_{代谢组学数据分析中，最常用的多维模型包括主成分分析（principal component analysis, PCA）、偏最小二乘法判别分析（Partial least squares discriminant analysis, PLS-DA）和正交偏最小二乘法判别分析（orthogonal PLS-DA, OPLS-DA）。PCA属于无监督的分类模型，可将多维的数据不断降维形成几个主要成分（PC）来尽可能描述原始数据的特征。其中PC1描述了原始数据矩阵中最显著的特征，PC2描述了除PC1之外最显著的数据特征，依此类推。PCA通常被用于寻找离群点（outlier）及观察不同组别之间的自然聚类趋势。那么如何判断数据集中的outlier？可通过Hotelling’s T2或PC1的score plot（PC1的数据解释率最高）来判断（图3），通常红线之外的样本为严重离群点，需要进一步处理。PCA的离群点也可以分组来看，以减少组间的干扰，如下图4所示。但对于离群点，不建议简单粗暴地删除，因为离群点通常是有趣且值得深究的。研究人员需要仔细地排查离群究竟是因为采样、前处理、检测等环节引入的误差还是客观的生物学差异引起的。}

​

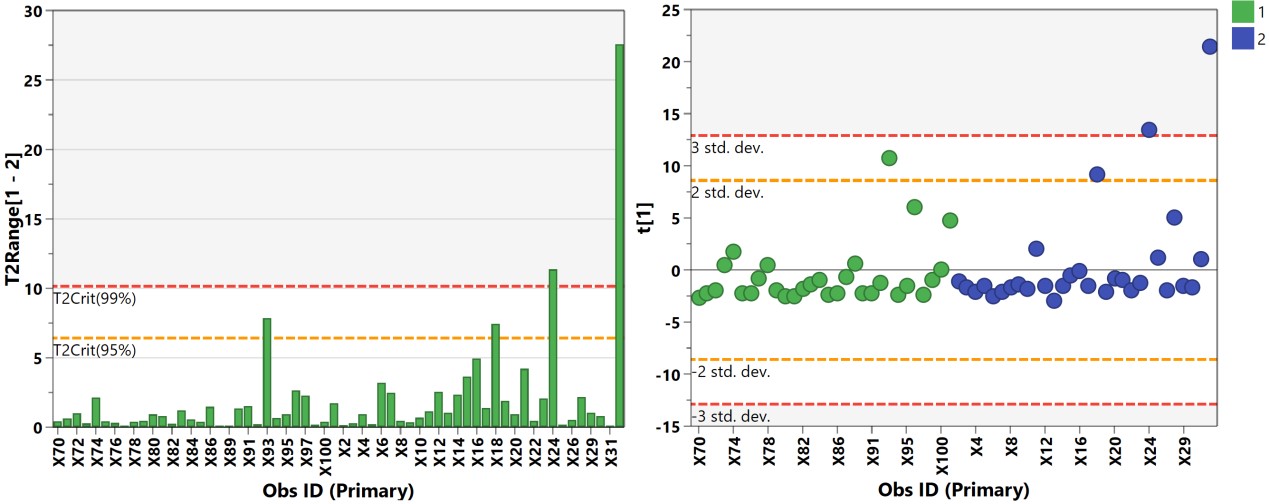
_{图3. Hotelling’s T2柱状图和PC1的得分图​​}

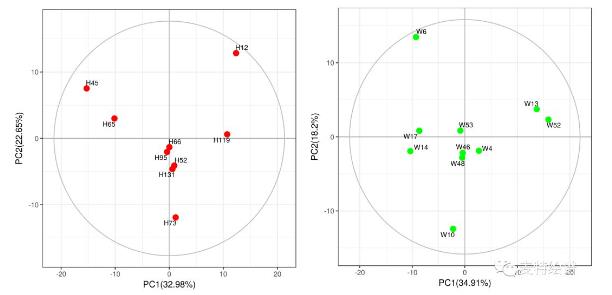
_{图4. 分组PCA 得分图用于离群点寻找。来  源：麦特绘谱XploreMET软件。​}

_{​利用PCA模型还可以观察样本间的自然聚类趋势。不同组别样本在PCA Score plot上即可分离是多维统计结果可靠性的最有力证据。然而，不同组别样本不一定都存在明显的差异，尤其对于临床样本的影响因素较多，如性别、年龄、BMI、地域、饮食、生活环境等。这些因素会给数据集带来很多和分组信息无关的噪音信号。此时，可以利用有监督的分类模型。有监督的意思就是事先告诉模型样本的真实分组信息再进行模型构建。PLS-DA能按照预先定义的分类（Y变量）最大化组间的差异，获得比PCA更好的分离效果（图5）。OPLS-DA综合了PLS-DA和正交信号过滤（orthogonal signal correction, OSC）技术，能够把与预先设定的和分类无关的信息最大程度从原始矩阵分离，从而将最相关的因素集中到第一个主成份（Predictive component）上，进而寻找该主成分的正交矫正轴方向，从而使得组间样本分离效果更佳，使组内差异弱化，组间差异最大化凸显，且更适用于两组样本间的分离。PLS-DA可以用于两组及以上组别的分类比较，而OPLS-DA通常用于两组的对比，找差异物质。}

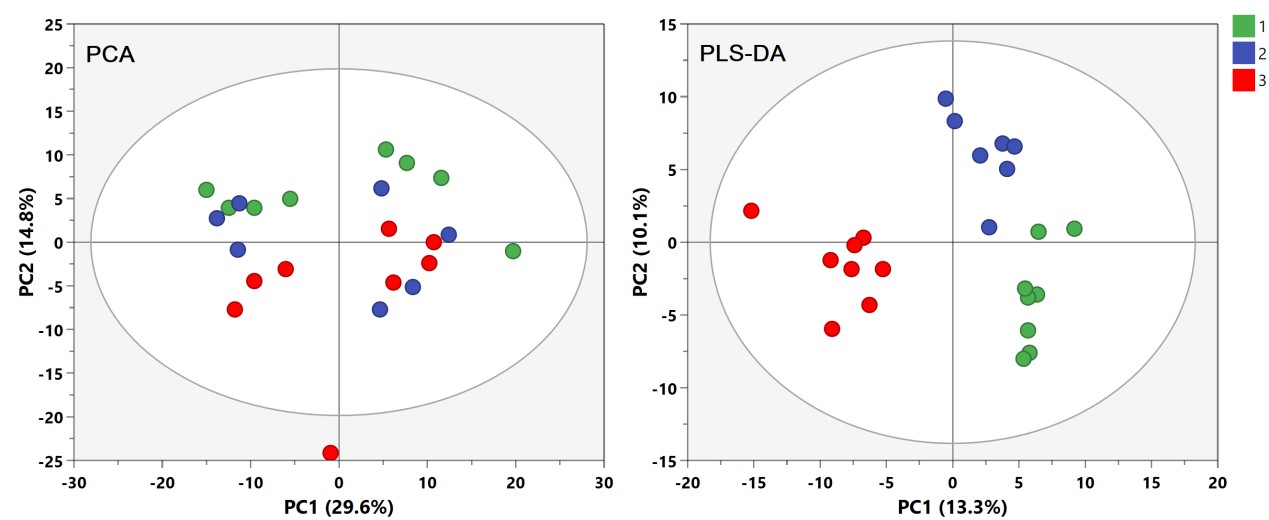
_{图5. PCA和PLS-DA得分图，PLS-DA可获得更清晰的分离​​}